SISTEMA POSICIONAL
El sistema de numeración que utilizamos normalmente, conocido como decimal, consta de diez símbolos (del 0 al 9) y es de tipo posicional. Esto significa que el valor de cada símbolo depende de la posición que ocupa.
En el caso del sistema decimal, el valor de cada posición se incrementa, hacia la izquierda, aumentando la potencia de la base (en este caso 10)
…| 105 | 104 | 103 | 102 | 101 | 100 |
Entonces, para el número 61803310 seria:
n = 6*105 +1*104 +8*103 +0*102 +3*101 +3*100
o bien:
n = 600000+10000+8000+0+30+3 = 61803310
SISTEMAS NO POSICIONALES

Existen otros sistemas con características diferentes, como por ejemplo el sistema de números Romanos, que no es posicional sino aditivo y sustractivo, ya que cada símbolo tiene un valor fijo que suma hacia la derecha y resta hacia la izquierda de uno mayor. Además, no tiene representación para el cero.

Veamos algunos ejemplos:
VII = 5+1+1 = 7
XL = -10+50 = 40
MCMLXXVIII = 1000+(-100+1000)+50+10+10+5+1+1+1 = 1978
MDCCCXVI = 1000+500+100+100+100+10+5+1 = 1816
MCDXCII = 1000+(-100+500)+(-10+100)+1+1 = 1492
El sistema de números romanos está basado en la numeración etrusca, que era solamente aditiva.
LOS NÚMEROS ARÁBIGOS

Volviendo a nuestro conocido sistema decimal, digamos que sus símbolos son conocidos como números arábigos, debido a su uso masivo en el medio oriente alrededor del siglo VI, aunque sus orígenes se remontan a la India y algunas especulaciones sostienen que un sistema posicional de diez símbolos ya era usado anteriormente en China.
Lo concreto es que los números arábigos fueron introduciéndose lentamente en la Europa medieval. Fibonacci, un matemático italiano que había estudiado en Bugía, hoy Argelia, contribuyó fuertemente a la difusión por Europa del sistema arábigo con su libro Liber Abaci, publicado en 1202.

Sin embargo, no fue sino hasta la invención de la imprenta en 1450, cuando este sistema de numeración comenzó a emplearse de forma generalizada en Europa. Ya para el siglo XV se utilizaba ampliamente, aunque los números arábigos finalmente reemplazaron a la numeración cirílica en Rusia recién alrededor de 1700, cuando fueron introducidos por el zar Pedro I de Rusia.

Números cirílicos 
La imprenta de Gutenberg
LOS NÚMEROS Y LAS COMPUTADORAS
Con el advenimiento de la Informática hacia la mitad del siglo XX comenzaron a usarse otros sistemas posicionales más adecuados que el decimal para el manejo de computadoras.
Tempranamente hubo intentos de desarrollos decimales cuando las primeras máquinas eran un desarrollo híbrido de mecánica (engranajes), electromecánica (relés) y electrónica (tubos de vacío o “válvulas”). Pero, conforme aumentaba su complejidad, esta tecnología se volvía inviable.

La ingeniería y la industria se volcaron al sistema binario y cuando las computadoras se volvieron 100% electrónicas, toda la Informática se transformó en “digital” y el dígito binario se convirtió en “bit” (acrónimo de binary digit).
Un bit representa algo que solo puede tomar uno de dos estados posibles, como, por ejemplo, encendido y apagado, sí y no, alto y bajo o positivo y negativo, por lo que resulta ideal para representar datos a través de los circuitos electrónicos y por lo tanto, para la Informática.
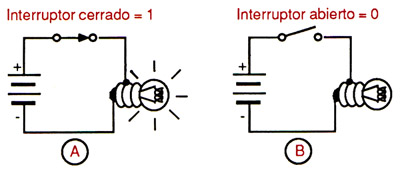
EL SISTEMA BINARIO
El sistema binario consta de solo dos símbolos (0 y 1) y es, como ya se dijo, posicional, así que del mismo modo que en el decimal, el valor de cada posición se incrementa, hacia la izquierda, aumentando la potencia de la base que en este caso es 2
…| 25 | 24 | 23 | 22 | 21 | 20 |
Supongamos que queremos saber el valor del numero binario 1001112
n = 1*32+0*16+0*8+1*4+1*2+1*1 = 3910
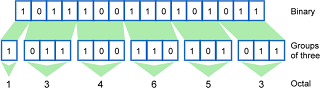
Como podemos intuir, los números binarios son muy largos, fáciles para las maquinas pero incomodos para los humanos. Para mejorar esta situación, es que se comenzó a trabajar con grupos de tres y cuatro bits, dando origen a los sistemas octal y hexadecimal respectivamente.
EL SISTEMA OCTAL
El sistema octal fue muy utilizado en las líneas de mini computadoras durante la segunda mitad del siglo XX, principalmente por DEC (Digital Equipment Corporation) en su línea PDP y sus sucesoras desde fines de los 60 hasta que fue comprada por Compaq en los 90 y esta a su vez por HP en 2002.

Aunque ahora está casi en desuso, el octal tiene la ventaja de la operación y comprensión simple, dada su visualización tan cercana al decimal. Es un sistema con ocho símbolos (del 0 al 7) y, por lo tanto de base 8.
…| 85 | 84 | 83 | 82 | 81 | 80 |
Para conocer el valor del número octal 507328 seria:
n = 5*84 +0*83 +7*82 +3*81 +2*80
n = 5*40964 +0*5123 +7*64+3*8+2*1
n = 20480+0+448+24+2 = 2095410
EL SISTEMA HEXADECIMAL
El sistema hexadecimal (también llamado “HEXA” o “HEX”) que llega a nuestros días fue introducido por IBM alrededor de 1967 y si bien tuvo fuertes competidores como el Octal e incluso el Decimal, dos décadas después ya se convertiría indefectiblemente en el estándar de la industria. Varios factores contribuyeron a esto, pero sin dudas el mas importante fue el tamaño del Byte.
Un Byte es un grupo de bits que, por decirlo de una manera, se mueven juntos, de manera que representan un valor o un dato en manera conjunta. En los circuitos de una computadora, estos bits viajan por carriles paralelos que forman un BUS (algo similar a una autopista) y parten de un punto y llegan a otro punto, todos a la vez, acarreando el dato (por ejemplo, una letra).
Tempranamente y dependiendo del objetivo o función, los Bytes fueron diseñados usando ocho, siete, seis e incluso cinco bits, pero conforme aumentaban y mejoraban los diseños, la tendencia de la industria comenzaba a estandarizar un Byte de ocho bits. Finalmente, en la década del 70 con la aparición del microprocesador de propósitos generales Intel 8080, seguido del Zilog Z80 y el Motorola 6800, todos ellos de ocho bits, la discusión por el tamaño del Byte terminó.

Z80 
MC6800 
8080
Ya, con un Byte de ocho bits estandarizado de facto, resultaba obvia la conveniencia del uso del sistema hexadecimal que podía representar un Byte exactamente con dos dígitos, sin faltantes ni desperdicio de bits.
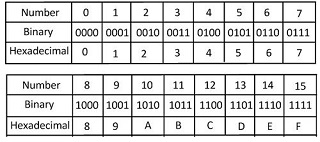
Así, podemos definir al HEXA como un sistema posicional que consta de 16 símbolos y por consiguiente es de base 16, ocupando exactamente cuatro dígitos binarios.
Los primeros diez símbolos son arábigos del 0 al 9 y luego continúan las leras latinas de la A hasta la F, representando A=10, B=11, C=12, D=13, E=14 y F=15
…| 165 | 164 | 163 | 162 | 161 | 160 |
Para conocer el valor el número 1A0F6E16 sería:
n = 1*165 +10*164 +0*163 +15*162 +6*161 +14*160
n = 1048576+655360+0+3840+96+14 = 170788610
EL PREFIJO 0x
Al principio de los años 70, en los laboratorios Bell, comenzaron a desarrollarse sobre equipos PDP-11 el sistema Unix y el lenguaje C. Este último surgió a raíz de la necesidad de contar con un lenguaje de alto nivel para escribir el sistema operativo que hasta ese momento se hacia en lenguaje ensamblador (instrucciones básicas de la máquina).
Este lenguaje, utilizaba en su sintaxis, el prefijo 0x para indicar que lo que seguía era un valor hexa. Así, por ejemplo el codigo ASCII para la letra M se escribe 0x4D y el número 1A0F6E16 sería entonces 0x1A0F6E.
El rápido avance y popularización de este lenguaje y sus sucesores convirtieron esta notación en un estandard que reemplazó de hecho el uso del sufijo 16, no solo en sintaxis de programación, sino también en cualquier texto de estudio o descripción y en la escritura cotidiana. Puede verse también que esta notación es mucho mas fácil y amigable de tipear.
MAS SISTEMAS POSICIONALES
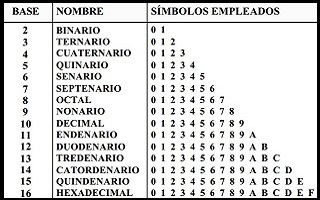
Como ya hemos visto, los sistemas más usados actualmente son el decimal, el binario y el hexadecimal. Sin embargo, aunque poco usados, existen sistemas con otras bases. Pensemos que perfectamente podríamos hacer un sistema de numeración con cualquier base que se nos ocurra. Veamos por ejemplo, la siguiente tabla:
MSB Y LSB
Al usar sistemas posicionales, sobre todo en el binario, en ocasiones es necesario indicar cuál es cada uno de los extremos del número, o sea, cual es la cifra más significativa y cuál es la menos significativa de la expresión.
En el uso del sistema binario se llaman MSB (Most Significant Bit) y LSB (Less Significant Bit). Es muy común encontrar estos indicadores en diagramas lógicos o electrónicos, consolas, displays y en algunas expresiones matemáticas.
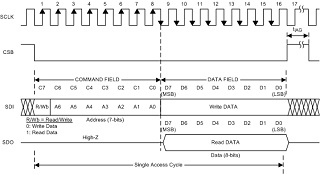
Diagrama de tiempos 
Diagrama de conexiones
DE BASE 10 A OTRAS BASES
Para convertir cualquier número decimal en un número de otra base existe un método muy sencillo.
Consiste en dividir nuestro número por la base, anotar el resto (que será nuestro LSB), volver a dividir el resultado por la base y así sucesivamente hasta que el resultado sea indivisible (será nuestro MSB).
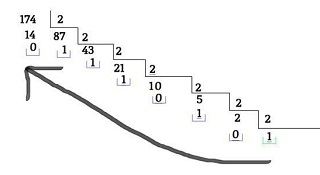
Por ejemplo, si queremos convertir el número 3910 en binario
39/2 = 19 >>> Resto = 1 (LSB)
19/2 = 9 >>> Resto = 1
9/2 = 4 >>> Resto = 1
4/2 = 2 >>> Resto = 0
2/2 = 1 >>> Resto = 0
>> Ultimo resultado = 1 (MSB)
Entonces 3910 = 1001112
Veamos un ejemplo mas gráfico:
Ahora veamos como lo haríamos para convertir el número 170788610 a hexadecimal.
1707886/16 = 106742 >> Resto = 14 = E
106742/16 = 6671 >> Resto = 6
6671/16 = 416 >> Resto = 15 = F
416/16 = 26 >> Resto = 0
26/16 = 1 >> Resto = 10 = A
>> Ultimo resultado = 1
Así obtenemos que 170788610 = 1A0F6E16
Como queda dicho, de la misma forma podríamos convertir números decimales a números de cualquier otra base.

